企業(yè)生存風(fēng)險如何預(yù)測,？
——
最近譽存科技的數(shù)據(jù)科學(xué)家們在模型開發(fā)中又取得了一項新的進展,。通過引進Cox回歸分析，進一步優(yōu)化了企業(yè)失信,、破產(chǎn)預(yù)測模型,，使得我們對企業(yè)風(fēng)險變化的預(yù)測，可以隨時間的變化而相應(yīng)變化,，最終獲得更為科學(xué)動態(tài)的預(yù)測結(jié)果,。
一、為什么選擇Cox回歸分析,？
Cox回歸模型,，又稱比例風(fēng)險回歸模型(Proportional hazards model）。1972年,，由英國統(tǒng)計學(xué)家D.R.Cox提出,，是一種半?yún)?shù)回歸模型。
該模型以生存結(jié)局和生存時間為應(yīng)變量,，可同時分析眾多因素對生存期的影響,。它不僅考慮事件是否發(fā)生，也考慮事件發(fā)生出現(xiàn)的時間,，能分析帶有截尾生存時間的數(shù)據(jù),，且不要求估計數(shù)據(jù)的生存分布類型。自問世以來,，Cox回歸在醫(yī)學(xué)隨訪研究中受到廣泛應(yīng)用,，是迄今生存分析中應(yīng)用最多的多因素分析方法。
?
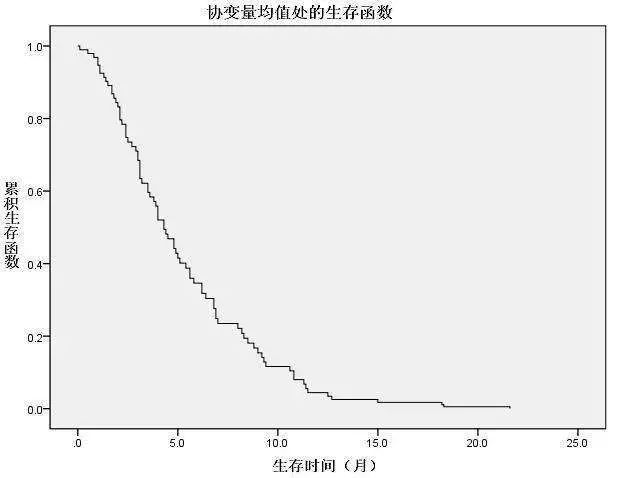
綜上所述,，我們可以很清晰的明了,，醫(yī)學(xué)隨訪研究與企業(yè)風(fēng)險預(yù)測其實在本質(zhì)上是相通的，都是關(guān)于主體生存資料的分析,。
同時,，我們也發(fā)現(xiàn),，那些基于常規(guī)分析模型所做的企業(yè)風(fēng)險預(yù)測，往往會存在兩個問題：
1,、歷史數(shù)據(jù)的標簽一般基于當前狀態(tài)來判斷,，沒有考慮時間的變量；
2,、模型輸出值僅為當前發(fā)生風(fēng)險的概率,，不涉及未來一段時間內(nèi)的風(fēng)險概率。
所以,，如果引入Cox回歸分析構(gòu)建關(guān)于企業(yè)生存的分析模型,，我們就能加入更多基于時間的變量因素，預(yù)測出未來一段時間內(nèi)企業(yè)發(fā)生失信,、破產(chǎn)等風(fēng)險的概率,。
?
二、Cox回歸模型的理論推導(dǎo)
Cox回歸模型的基本原理
生存分析是將結(jié)局或終點事件和出現(xiàn)這一結(jié)局所經(jīng)歷的時間結(jié)合起來分析的一種統(tǒng)計方法,。
?
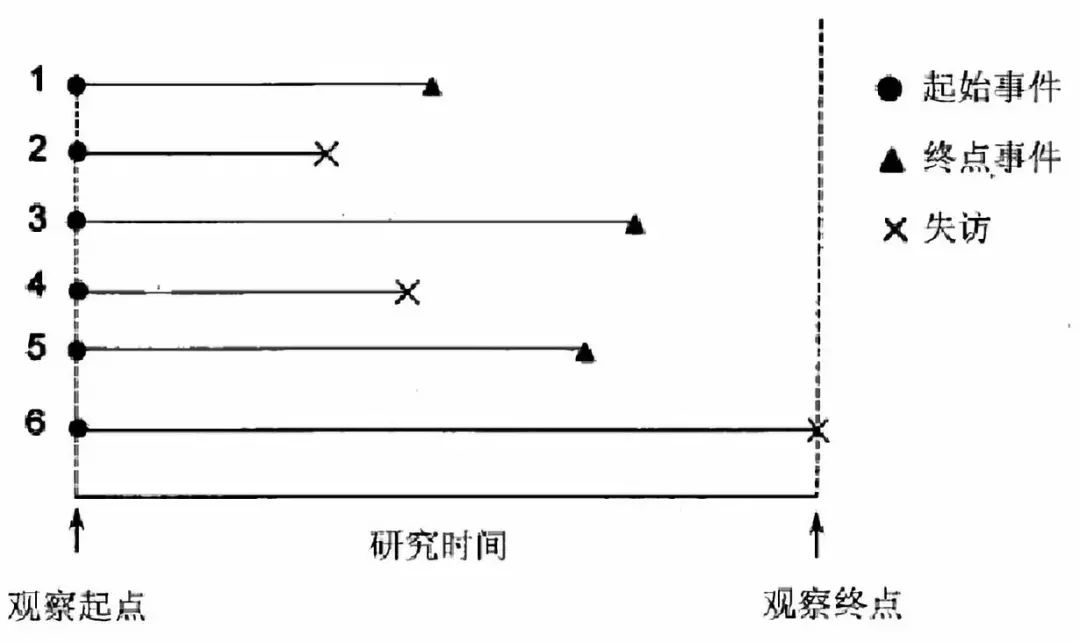
首先,，我們需要明確生存分析中常用的6個術(shù)語，如下：
（1）起始事件：反應(yīng)研究對象開始生存過程的起始特征事件,。 ????????
（2）終點事件：出現(xiàn)研究者所關(guān)心的特定結(jié)局,。
（3）觀察時間：從研究開始觀察到研究觀察結(jié)束的時間。
（4）生存時間：觀察到的存活時間,。
（5）完全數(shù)據(jù)：從觀察起點到死亡事件所經(jīng)歷的時間,，生存時間是完整的。
（6）截尾數(shù)據(jù)：觀察時間不是由于終點事件而結(jié)束的,，而是由于失訪,、死于非研究因素、觀察結(jié)束以上三種原因結(jié)束而對象仍存活的,。
?
Cox回歸分析的一般條件
①比例風(fēng)險假定：即PH假定,，常通過觀察自變量分組的Kaplan-Meier生存曲線。若曲線無明顯的交叉,，則提示滿足PH假定,。
②樣本含量：一般需要協(xié)變量的15~20倍的陽性結(jié)局事件數(shù)。
?
Cox回歸的風(fēng)險函數(shù)公式
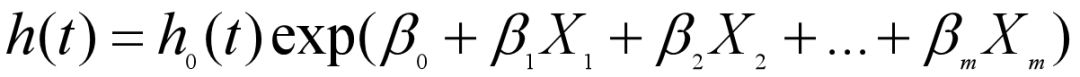
其中,，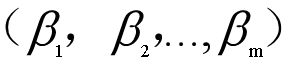
是線性模型的系數(shù)(未知參數(shù)),，
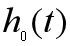是基準風(fēng)險函數(shù)，exp(...)這個式子描述了企業(yè)主體觀察到回歸變量
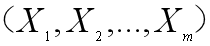的破產(chǎn)風(fēng)險比例,；式中h(t)是具有協(xié)變量x的個體在時刻t的風(fēng)險函數(shù),，t表示生存時間。?i∈N,βi>0,，表示該協(xié)變量是危險因素,，越大使得生存時間越短,。?i∈N,βi
?
三、Cox回歸模型的應(yīng)用案例
我們的模型研究以企業(yè)發(fā)生失信或破產(chǎn)為結(jié)局,，各類風(fēng)險參數(shù)為主要研究因素,，欲了解哪個參數(shù)對企業(yè)主體的生存影響更大，即可應(yīng)用Cox比例風(fēng)險模型進行分析,。
下面,，以企業(yè)破產(chǎn)風(fēng)險預(yù)測為例：
>>> 預(yù)測某公司在未來時間段的破產(chǎn)概率
1. 樣本
正樣本：2W個 （隨機抽取的未破產(chǎn)公司）
負樣本：3707個 （從破產(chǎn)公告中解析出來）
2. 提取特征
包含司法類、股東類,、法人類、工商類等數(shù)十個特征
3. 訓(xùn)練模型
模型的數(shù)據(jù)預(yù)處理流程跟一般的模型分析類似,，如下圖所示：
本次模型構(gòu)建最優(yōu)訓(xùn)練步長為0.05, 得到模型的綜合評價指標Concordance =0.756,，表明具有較好的區(qū)分度。同時,，從模型的輸出結(jié)果可以看出最終有14個特征具有統(tǒng)計學(xué)上顯著意義,。比如，一個企業(yè)作為被告身份涉及的訴訟次數(shù)（defendant_judgedoc_cnt）,，法人的關(guān)聯(lián)企業(yè)涉及的執(zhí)行次數(shù)（network_fr_zhixing_cnt）對企業(yè)風(fēng)險影響較大,。
進一步地，利用Cox模型我們還可以考察單一因素對企業(yè)風(fēng)險的影響,，例如：
（1）“成立年限”對破產(chǎn)預(yù)測模型的影響：成立年限越長,，其相對的風(fēng)險越大。
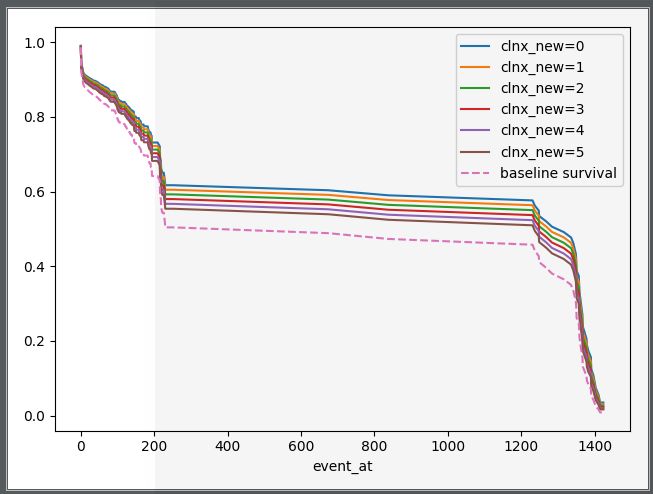
（2）“股東變更次數(shù)”對企業(yè)破產(chǎn)風(fēng)險的影響：股東變更次數(shù)越多對企業(yè)風(fēng)險影響也越大,。
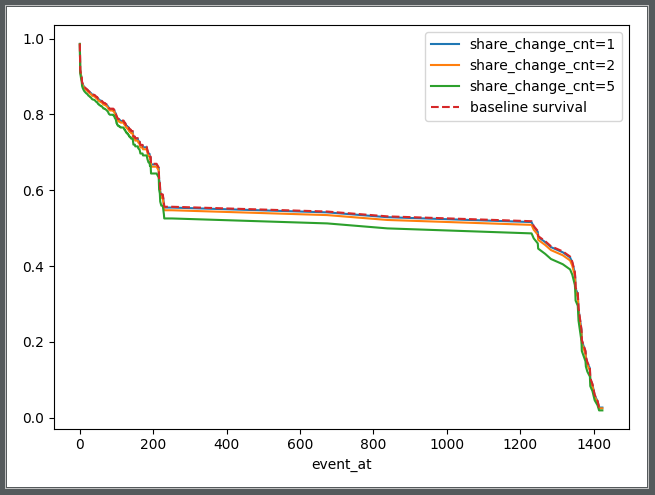
此外,，需了解一點。在實際應(yīng)用中,，Cox回歸的結(jié)局不一定就是破產(chǎn)或者失信,，還可能表現(xiàn)為跑路、行政處罰,、工商吊銷等,，不同的時間周期會表現(xiàn)出不一樣的結(jié)果。
四,、備注
在進行Cox回歸分析前,，如果樣本不多而變量較多，建議先通過單變量分析考察所有自變量與因變量之間的關(guān)系,，篩掉一些可能無意義的變量,，再進行多因素分析，以保證結(jié)果更加可靠,。另外,，即使樣本足夠大,，也不建議把所有的變量放入方程直接分析，一定要先弄清楚各個變量之間的相互關(guān)系,，確定自變量進入方程的形式,，這樣才能進行有效的分析。
?